Ejercicio 61.
3) Sumar x²-3xy con 3xy-y² y el resultado restarlo de x².
x²-3xy
. 3xy-y²
x² -y²
x²
-x² y²
. y² Solución.
__________________________________
4) ¿Qué expresión hay que añadir a 3x²-5x+6 para que la suma sea 3x?
Restando 3x²-5x+6 a 3x
. 3x
-3x²+5x-6
-3x²+8x-6 ← expresión a añadir.
Comprobando:
3x² -5x +6
-3x²+8x -6
. 3x Total.
__________________________________
5) Restar -2a²+3a-5 de 3 y sumar el resultado con 8a+5.
. 3
2a² -3a +5
2a² -3a +8
2a² - 3a +8
. 8a +5
2a² +5a+13 Solución.
__________________________________
. ___
6) Simplificar -3x²-{-[4x²+5x-(x²-x+6)]}
. __
= -3x²-{-[4x²+5x-(x²-x-6)]} Se suprimió la barra
= -3x²-{-[4x²+5x-x²+x+6]} Se suprimieron los paréntesis
= -3x²-{-[3x²+6x+6]} Se efectuaron operaciones
= -3x²-{-3x²-6x-6} Se suprimieron los corchetes
= -3x²+3x²+6x+6 Se suprimieron las llaves y se operó.
= 6x+6 Solución.
__________________________________
7) Simplificar (x+y)(x-y)-(x+y)²
= x² -y² - (x²+2xy+y²)
= x² -y² -x²-2xy-y²
= -2xy-2y² ó
= -2y² -2xy Solución.
___________________________________
8) Valor numérico de 3(a+b)-4(c-b)+√(c-b /-a) siendo a = 2, b = 3, c = 1
= 3(2+3)-4(1-3)+√(1-3 /-(2))
= 3(5) - 4(-2) + √(-2 /-2)
= 15 +8 + √1
= 23 +1
= 24 Solución.
___________________________________
9) Restar x²-3xy+y² de 3x²-5y² y sumar la diferencia con el resultado de restar 5xy+x² de 2x²+5xy+6y².
Primera resta:
3x² -5y²
- x² +3xy - y²
2x² +3xy -6y² diferencia.
Segunda resta:
2x² +5xy +6y²
- x²- 5xy .
. x² +6y² diferencia.
Suma de diferencias:
2x² +3xy -6y²
. x² +6y²
3x²+3xy Solución.
___________________________________
10) Multiplicar 2/3a² -1/2ab +1/5b² por 1/2a² +3/4ab -2b²
2/3a² -1/2ab +1/5b²
1/2a² +3/4ab -2b² .
1/3a⁴-1/4a³b + 1/10a²b²
. 1/2a³b - 3/8a²b² + 3/20ab³
. - 4/3a²b² + 1 ab³ -2/5b⁴
1/3a⁴+1/4a³b -193/120a²b² +23/20ab³ -2/5b⁴ Solución.
_____________________________________
11) Dividir la suma de x⁵-x³+5x², -2x⁴+2x²-10x, 6x³-6x+30 entre x²-2x+6
x⁵ - x³ +5x²
. -2x⁴ +2x² - 10x
. +6x³ - 6x +30
x⁵- 2x⁴ +5x³ +7x² - 16x +30
. x³ -x +5 . ← Solución.
x²-2x+6 | x⁵- 2x⁴ +5x³ +7x² - 16x+30
. - x⁵+2x⁴ - 6x³
. -x³ +7x² -16x
. x³ -2x² + 6x
. 5x² -10x +30
. -5x²+10x - 30
. 0
______________________________________
12) Restar el cociente de 1/4a³-1/90ab²+1/15b³ entre 1/2a+1/3b de 1/2a²+ab+1/5b²
. 1/2a² -1/3ab +1/5b² .
1/2a+1/3b | 1/4a³ -1/90ab² +1/15b³
. -1/4a³-1/6a²b
. -1/6a²b -1/90ab²
. 1/6a²b +1/9 ab²
. 1/10ab² +1/15b³
. -1/10ab² -1/15b³
. 0
1/2a² + ab+1/5b²
-1/2a² +1/3ab -1/5b²
. 4/3ab ← Solución.
______________________________________
13) Restar la suma de -3ab²-b³ y 2a²b+3ab²-b³ de a³-a²b+b³ y la diferencia multiplicarla por a²-ab+b².
Sumando:
. -3ab²- b³
2a²b+3ab²- b³
2a²b -2b³
Restando:
a³- a²b+ b³
. -2a²b+2b³
a³-3a²b+3b³
Multiplicando:
a³-3a²b+3b³
a² -ab +b² .
a⁵-3a⁴b +3a²b³
- a⁴b+3a³b² -3ab⁴
. + a³b²- 3a²b³ +3b⁵
a⁵-4a⁴b+4a³b² -3ab⁴+3b⁵
a⁵-4a⁴b+4a³b² -3ab⁴+3b⁵ Solución.
___________________________________
14) Restar la suma de x³-5x²+4x, -6x²-6x+3, -8x²+8x-3 de 2x³-16x²+5x+12 y dividir esta diferencia entre x²-x+3.
Sumando:
x³ - 5x² +4x
. - 6x² - 6x +3
. - 8x² +8x - 3
x³ -19x² +6x
Restando:
2x³ - 16x²+5x+12
- x³ +19x² -6x .
. x³ + 3x² - x +12
Dividiendo:
. x +4 .
x² -x +3 | x³ +3x² - x +12
. - x³+ x² - 3x
. 4x² - 4x
. -4x² +4x -12
. 0
x + 4 Solución.
___________________________________
15) Probar que (2+x)²(1+x²)-(x²-2)(x²+x-3) = x²(3x+10)+2(3x-1)
1°) (2+x)²(1+x²)-(x²-2)(x²+x-3)
= (4+4x+x²)(1+x²) - (x⁴-4x²+4)(x²+x-3)
= (4+4x+x²+4x²+4x³+x⁴) - (x⁴+x³-3x²-2x²-2x+6)
= (x⁴+4x³+5x²+4x+4) - (x⁴+x³-5x²-2x+6)
. x⁴+4x³+ 5x²+4x+4
-x⁴ - x³+ 5x²+2x-6
. 3x³+10x²+6x-2
2°) x²(3x+10)+2(3x-1)
= 3x³+10x²+6x-2
⇒
(2+x)²(1+x²)-(x²-2)(x²+x-3) = x²(3x+10)+2(3x-1)
3x³+10x²+6x-2 = 3x³+10x²+6x-2 Comprobado.
___________________________________
16) Hallar el valor numérico de (x+y)²(x-y)²+2(x+y)(x-y) ,
siendo x = -2, y = 1
=[-2+1]²[-2-(1)]²+2[-2+1][-2-(1)]
= (-1)²(-3)²+2(-1)(-3)
= (1)(9)+2(-1)(-3)
= 9 +6
= 15. Solución.
___________________________________
17) ¿Qué expresión hay que sumar a la suma de x+4, x-6 y x²+2x+8 para obtener 5x²-4x+3?
Sumando:
x²+2x+ 8
. x+ 4
. x - 6
x²+4x+ 6
Restando:
5x²-4x+ 3
- x²-4x - 6
4x²-8x - 3 ← expresión a sumar.
Comprobando:
. x²+4x+ 6
4x² -8x - 3
5x² -4x +3 ← Comprobado.
___________________________________
18) Restar -{3a+(-b+a)-2(a+b)} de -2[(a+b)-(a-b)]
Suprimiendo signos de agrupación y simplificando:
= -{3a+(a-b)-2(a+b)} ; -2[(a+b)-(a-b)]
= -{3a+a-b-2a-2b} ; -2[a+b-a+b]
= -{2a-3b} ; -2a-2b+2a-2b
= -2a+3b ; -4b
⇒Restando:
-4b
2a-3b
2a-7b Solución.
___________________________________
. ___
19) Multiplicar 5x+[-(3x -x-y)] por 8x+[-2x+(-x+y)]
Suprimiendo signos de agrupación:
. ___
= 5x+[-(3x -x-y)] ; 8x+[-2x+(-x+y)]
= 5x+[-(3x-x+y)] ; 8x+[-2x-x+y]
= 5x+[-3x+x-y] ; 8x+[-3x+y]
= 5x-3x+x-y ; 8x-3x+y
= 3x-y ; 5x+y
⇒Multiplicando:
3x-y
5x+y
15x²-5xy
. 3xy-y²
15x²-2xy-y² Solución.
__________________________________
20) Restar el cociente de 1/4x³+1/24x²y+5/12xy²+1/3y³ entre 1/2x²-1/4xy+y² de 2x+[-5x-(x-y)]
Dividiendo:
. 1/2x +1/3y .
1/2x²-1/4xy+y² | 1/4x³+1/24x²y+ 5/12xy²+1/3y³
. -1/4x³+ 1/8 x²y - 1/2xy²
. 1/6 x²y - 1/12xy²
. -1/6 x²y + 1/12xy²-1/3y³
. 0
Simplificando el minuendo:
2x+[-5x-(x-y)]
= 2x+[-5x-x+y]
= 2x-5x-x+y
= -4x+y
Restando:
- 4x + y
-1/2x - 1/3y
-9/2x +2/3y Solución.
__________________________________
21) Probar que [x²-(3x+2)][x²+(-x+3)] = x²(x²-4x+4)-(7x+6)
1°) [x²-(3x+2)][x²+(-x+3)]
= [x²-3x-2][x²-x+3]
= x⁴-x³+3x²-3x³+3x²-9x-2x²+2x-6
= x⁴-4x³+4x²-7x-6
2°) x²(x²-4x+4) - (7x+6)
= x⁴-4x³+4x²-7x-6
⇒
[x²-(3x+2)][x²+(-x+3)] = x²(x²-4x+4)-(7x+6)
es equivalente a:
x⁴-4x³+4x²-7x-6 = x⁴-4x³+4x²-7x-6 Comprobado.
__________________________________
22) ¿Qué expresión hay que sumar al producto de [x(x+y)-x(x-y)][2(x²+y²)-3(x²-y²)] para obtener 2x³y+3xy³?
Simplificando:
[x(x+y)-x(x-y)][2(x²+y²)-3(x²-y²)]
= [x²+xy-x²+xy][2x²+2y²-3x²+3y²]
=[2xy][-x²+5y²]
Multiplicando:
-x²+5y²
2xy .
-2x³y+10xy³
Restando:
2x³y+ 3xy³
2x³y-10xy³
4x³y- 7xy³ expresión a sumar.
Comprobando:
- 2x³y+10xy³
. 4x³y - 7xy³
. 2x³y+ 3xy³ comprobado.
________________________________
23) Restar -x²-3xy+y² de 0 y multiplicar la diferencia por el cociente de dividir x³-y³ entre x-y.
Restando:
0
x²+3xy-y²
x²+3xy-y² Diferencia.
Dividiendo:
. x²+xy+y² . Cociente.
x -y | x³ -y³
. -x³+x²y
. x²y
. -x²y+xy²
. xy²
. -xy²+y³
. 0
Multiplicando:
x²+3xy-y²
x²+xy+y²
x⁴+3x³y -x²y²
x³y+3x²y² - xy³
. x²y²+3xy³ -y⁴
x⁴+4x³y+3x²y²+2xy³ -y⁴ Solución.
__________________________________
24) Simplificar (x-y)(x²+xy+y²) - (x+y)(x²-xy+y²)
= (x-y)(x²+xy+y²) - (x+y)(x²-xy+y²)
Multiplicando 1°:
x²+xy+y²
x -y .
x³+x²y+xy²
. -x²y -xy² -y³
x³ -y³
Multiplicando 2°
x³-x²y+xy²
. x²y -xy² +y³
x³ +y³
⇒
(x-y)(x²+xy+y²) - (x+y)(x²-xy+y²)
= (x³ -y³) - (x³ +y³)
= x³ - y³
. -x³ - y³
. -2y³ Solución.
__________________________________
25) Hallar el valor numérico de √ab /c +2(b-a)√9b /a² -3(c-b)√c/b,
siendo a = 4, b = 9, c = 25
= √(4)(9) /25 +2(9-4)√9(9) /(4)² -3(25-9)√25/9
= √36/25 +2(5)√81/16 -3(16)√25/9
= 6/5 +10(9/4)-48(5/3)
= 6/5 +90/4 -80
= 237/10 -80
= -563/10
= -56 ³/₁₀ Solución.
___________________________________
26) ¿Por cuál expresión hay que dividir el cociente de x³+3x²-4x-12 entre x+3 para obtener x-2?
. x²-4 .
x +3 | x³+3x²-4x-12
. -x³-3x²
. 0 -4x-12
. 4x+12
. 0
Dividiendo el cociente encontrado (x²-4) entre la expresión que se quiere obtener (x-2), para obtener la expresión por la que hay que dividir el cociente encontrado.
. x+2 .
x-2 | x² -4
. -x²-2x
. -2x -4
. 2x+4
. 0
Solución: La expresión a la que hay que dividir es x+2.
Comprobando:
. x-2 .
x+2 | x² -4
. -x²-2x
. -2x -4
. 2x+4
. 0
___________________________________
. ___
27) Simplificar 4x²-{3x-(x² - 4+x)}+[x²-{x+(-3)}] y hallar su valor para x = -2.
.
= 4x²-{3x-(x²-4-x)}+[x²-{x-3}]
= 4x²-{3x-x²+4+x}+[x²-x+3]
= 4x²+x²-4x-4+[x²-x+3]
= 4x²+x²-4x-4+x²-x+3
= 6x²-5x-1
Valor numérico de 4x²-5x-1, siendo x=-2
= 6(-2)²-5(-2)-1
= 6(4) +10 -1
= 24 +10 -1
= 33. Solución.
____________________________________
28) ¿De cuál expresión hay que restar -18x³+14x²+84x-45 para que la diferencia dividida entre x²+7x-5 dé como resultado x²-9?
Multiplicando el divisor x²+7x-5 por el cociente x²-9, para encontrar el dividendo, que será la expresión a la que se restará (minuendo).
(x²+7x-5)(x²-9) = x⁴+7x³-14x²-63x+45
Restando:
x⁴+ 7x³ -14x² -63x+45
. -18x³+14x²+84x -45
x⁴ -11x³ 0 +21x 0
Solución: la expresión es x⁴ -11x³+21x
_____________________________________
29) Probar que (a²+b²)(a+b)(a-b) = a⁴-[3a+2(a+2)-4(a+1)-a+b⁴]
= (a²+b²)(a²-b²) = a⁴-[3a+2a+4-4a-4-a+b⁴]
= a⁴-b⁴ = a⁴-3a-2a-4+4a+4+a-b⁴
= a⁴ -b⁴ = a⁴+5a-5a-b⁴
= a⁴ -b⁴ = a⁴ -b⁴
⇒
(a²+b²)(a+b)(a-b) = a⁴-[3a+2(a+2)-4(a+1)-a+b⁴]
es equivalente a
. a⁴ - b⁴ = a⁴ - b⁴ Comprobado.
_____________________________________
30) Restar -x³-5x²+6 de 3 y sumar la diferencia con la suma de x²-x+2 y -[x²+(-3x+4) - (-x+3)]
Restando:
. 3
x³ +5x² -6
x³ +5x² -3 Diferencia
Sumando:
x²-x+2 + -[x²+(-3x+4) - (-x+3)]
= x²-x+2 + -[x²-3x+4+x-3]
= x²-x+2 -x²+3x-4-x+3
= x+1 total.
Sumando diferencia con total
x³ +5x² -3
. +x +1
x³ +5x² +x -2 Solución.
_____________________________________
 , es divisible, si "n" es impar.
, es divisible, si "n" es impar.  , no es divisible, si "n" es par
, no es divisible, si "n" es par , es divisible, si "n" es par.
, es divisible, si "n" es par. , nunca es divisible, ya sea "n" par o impar.
, nunca es divisible, ya sea "n" par o impar.

















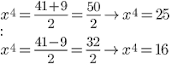
 son:
son:



