Son las ecuaciones que constan de tres términos: en donde el primer término es el doble en su exponente que el segundo, y el tercer término es independiente.
 , en donde a y b son los coeficientes del primer y tercer término respectivamente; c es el término independiente; n es el exponente al que está elevado la variable x, y 2n indica el doble del primer término con el siguiente.
, en donde a y b son los coeficientes del primer y tercer término respectivamente; c es el término independiente; n es el exponente al que está elevado la variable x, y 2n indica el doble del primer término con el siguiente.
Las ecuaciones trinomias en las que el primer término es x⁴, y el segundo x² se llaman ecuaciones bicuadráticas.
______________________________________
Ejemplo a) Resuelve x⁶-19x³ -216 = 0
Utilizando la fórmula de la ecuación de 2° grado:
Descomponiendo el término cuadrático x⁶ en (x³)², entonces:


Por lo tanto ( ∴ ),

Extraemos la raíz cúbica, para encontrar el valor de x:
x³ = 27 ∴ x = ∛27 ⇒ x = 3
x³ = -8 ∴ x = ∛-8 ⇒ x = -2
Igualando a cero los resultados de:
x³ = 27 ⇒ x³ -27 = 0
x³ = -8 ⇒ x³ +8 = 0
La expresión queda así:
(x³ -27)(x³ +8) = 0
Descomponiendo los factores x³ -27:
x³ -27 = (x-3)(x²+3x+9)
Igualando a cero los nuevos factores:
Si x-3 = 0 ⇒ x = 3
Si x² +3x +9= 0
∴
Descomponiendo los factores x³ +8:
x³ +8 = (x+2)(x²-2x+4)
Igualando a cero los nuevos factores:
Si x+2 = 0 ⇒ x = -2
∴
 raíces imaginarias.
raíces imaginarias.
Entonces las raíces de x⁶-19x³ -216 = 0 son
x=3 , x=-2 , x= -3/2+3√3i /2 , x= -3/2-3√3i /2 , x= 1+√3i , 1-√3i
______________________________________
Ejemplo b) Resolver 
Factorizando el trinomio:
Igualando a cero el primer factor:
Igualando a cero el segundo factor:
Las raíces de  son:
son:
_____________________________________
Ejercicio 184
Resolver las ecuaciones:

Utilizando la fórmula general:
Por lo tanto:
Igualando a cero:
Factorizando
1°.

 raíz
raíz raíces
raíces2°. 
 raíz.
raíz.Por lo tanto:
 raíces.
raíces.
Las raíces de  son:
son: _____________________________________
Por fórmula general:

Por lo tanto:
Igualando a cero y factorizando los resultados de x⁴:
1°. Si x⁴ = 25 ⇒ x⁴ -25 = 0 ⇒ (x²-5) (x²+5) = 0
Entonces:
Si x²-5 = 0 ⇒ x² = 5 ⇒ x = ±√5 Raíces.
Si x²+5 = 0 ⇒ x² = -5 ⇒ x = ±√-5 ⇒ x = ±√5i Raíces.
2°. Si x⁴ = 16 ⇒ x⁴ -16 = 0 ⇒ (x² -4) (x² +4) = 0
Entonces:
Si x² -4 = 0 ⇒ x² = 4 ⇒ x = ±√4 ⇒ x = ±2 Raíces.
Si x² +4 = 0 ⇒ x² = -4 ⇒ x = ±√-4 ⇒ x = ±√4i ⇒ x = ±2i Raíces.
Las raíces de  son:
son: ______________________________________
Despejando por la fórmula de 2° grado
Factorizando:
Si x⁵ =32 ⇒ x = √32 ⇒ x = 2 Raíz
Si x⁵ = 1 ⇒ x = √1 ⇒ x = 1 Raíz
Solución: Las raíces de la ecuación original son: x = 2 y x = 1.
____________________________________
Por lo tanto:
Factorizando el trinomio:
Por lo tanto;
Descomponiendo los factores:
 raíces
raíces.
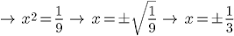 raíces
raíces.
Solución: Las raíces de la ecuación original son:
_________________________________________
Factorizando
Igualando a cero los factores:
 Raíz.
Raíz. Raíz.
Raíz.Solución: Las raíces de la ecuación son: x = 1/3 y x = -1.
_________________________________
Factorizando:
(x-9)(x-4) = 0
⇒
x -9 = 0 ⇒ x = 9
x -4 = 0 ⇒ x = 4
Solución: {x = 9 , x = 4}
Nota: 9 es una solución falsa y 4 es verdadera.
____________________________________
Factorizando por Fórmula de 2° grado:
Por lo tanto
⇒
Solución: {x = 16 , x = 1/16}
______________________________________
, en donde a y b son los coeficientes del primer y tercer término respectivamente; c es el término independiente; n es el exponente al que está elevado la variable x, y 2n indica el doble del primer término con el siguiente.

 raíz
raíz
 raíz.
raíz.
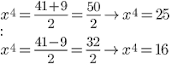
 son:
son:






No hay comentarios.:
Publicar un comentario
Sugiere, solicita o comenta. Es muy importante.