Valor numérico de una expresión algebraica es el resultado obtenido al sustituir las letras o variables por valores numéricos dados, luego de efectuadas las operaciones indicadas.
Valor numérico de expresiones simples.
Ejercicio 11.
Hallar el valor numérico de las siguientes expresiones; cuando
a = 1, b = 2, c = 3, m = 1/2, n = 1/3, p = 1/4
1) 3ab.
Sustituyendo y operando:
3(1)(2) = 6 Solución.
___________________________________
2) 5a²b³c
Sustituyendo y operando:
= 5(1²)(2³)(3)
=5(1)(8)(3)
= 120. Solución.
___________________________________
3) b²mn
= (2²)(1/2)(1/3)
= (4)(1/6)
= 2/3 Solución.
___________________________________
4) 24m²n³p
= 24(1/2)²(1/3)³(1/4)
= 24(1/4)(1/27)(1/4)
= 24(1/16)(1/27)
= 24(1/432)
= 1/18 Solución.
___________________________________
5) 2/3a⁴b²m³
= 2/3(1)⁴(2)²(1/2)³
= 2/3(1)(4)(1/8)
= (8/3)(1/8)
= 1/3 Solución.
___________________________________
6) 7/12(c)³(p)²(m)
= (7/12)(3)³(1/4)²(1/2)
= (7/12)(27)(1/16)(1/2)
= 27(7/384)
= 63/128 Solución.
___________________________________
7) mbncpa
= (1/2)²(1/3)³(1/4)¹
= (1/4)(1/27)(1/4)
= 1/432 Solución.
___________________________________
8) 5/6ab-1mc-2
= 5/6(1)²⁻¹(1/2)³⁻²
= 5/6(1)¹(1/2)¹
= (5/6)(1)(1/2)
= 5/12 Solución.
___________________________________
9) √2bc²
= √2(2)(3)²
= √(2)(2)(9)
= √36
= 6 Solución.
___________________________________
10) 4m∛12bc²
= 4(1/2)∛(12)(2)(3)²
= 2∛(12)(2)(9)
= 2∛216
= (2)(6)
= 12 Solución.
___________________________________
11) mn√8a⁴b³
= (1/2)(1/3)√(8)(1)⁴(2)³
= (1/6)√(8)(1)(8)
= (1/6)√64
= (1/6)(8)
= 4/3 Solución.
___________________________________
12) 4a / 3bc
= 4(1) / (3)(2)(3)
= 4/18
= 2/9 Solución.
___________________________________
13) 5b²m² /np
= (5)(2)²(1/2)² /(1/3)(1/4)
= (5)(4)(1/4) /(1/3)(1/4)
= 5/ 1/12
= 60 Solución.
___________________________________
14) 3/4b³ / 2/3c²
= (3/4)(2)³ / (2/3)(3)²
= (3/4)(8) / (2/3)(9)
= 6/6
= 1. Solución.
___________________________________
15) 2m / √n²
= (2)(1/2) / √(1/3)²
= 1 / √1/9
= 1/ 1/3
= 3 Solución.
___________________________________
16) 24mn / 2√n²p²
= (24)(1/2)(1/3) / 2√(1/3)²(1/4)²
= (24)(1/6) / 2√(1/9)(1/16)
= 4 / 2√1/144
= 4/ (2)(1/12)
= 4/ 1/6
= 24 Solución.
____________________________________
17) 3∛64b³c⁶ / 2m
= 3∛(64)(2)³(3)⁶ / (2)(1/2)
= 3∛(64)(8)(729) / 1
= 3∛373248 / 1
= 3(72)/1
= 216 Solución.
_____________________________________
18) 3/5√apb² / (3/2)∛125bm
= 3/5√(1)(1/4)(2)² / (3/2)∛(125)(2)(1/2)
= 3/5√(1)(1/4)(4) / (3/2)∛(125)(2)(1/2)
= 3/5√1 / (3/2)∛125
= (3/5)(1) / (3/2)(5)
= 3/5 / 15/2
= 2/25 Solución.
_____________________________________







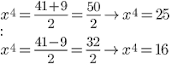
 son:
son:



