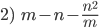Reducción de una expresión mixta a fraccionaria.

Procedimiento:
1. Se multiplica la parte entera por el denominador de la fracción.
2. El resultado se le suma o resta el numerador, según el signo que antecede a la fracción.
3. Todas estas operaciones se parten por el denominador.
4. Si es posible se simplifica el resultado.
_______________________________________

Ejemplos:
 a) Reducir a una sola fracción 

Multiplicando la parte entera por el denominador:

Efectuando operaciones del numerador y simplificando:

______________________________________

b) Reducir a una sola fracción:

  

Multiplicando la parte entera por el denominador:

Efectuando operaciones y simplificando:

_______________________________________

c) Reducir a una sola fracción: 

Multiplicando la parte entera por el denominador:

Efectuando operaciones y simplificando:

_________________________________________

Ejercicio 124.

Reducir a una sola fracción:

_____________________________________

______________________________________

_______________________________________

________________________________________

________________________________________

________________________________________

_________________________________________

__________________________________________

___________________________________________

____________________________________________

____________________________________________

Simplificación de fracciones cuyos términos no pueden factorarse fácilmente.

Regla:  Hallar el m.c.d. del numerador y denominador por divisiones sucesivas y dividir el numerador y el denominador por el m.c.d. de la fracción.

______________________________________

Ejemplo: Simplificar

   

Hallando el m.c.d. del numerador entre el denominador:

.                               x                                  .

x⁵-2x⁴+6x³-2x²+5x |  x⁶- 2x⁵+5x⁴-  x³+2x²-5x

.                               -x⁶+2x⁵- 6x⁴+2x³-5x²

.                                           -   x⁴+  x³-3x²-5x  → ÷ -1 = x⁴-x³+3x²+5x

.                       x-1                         .

x⁴-x³+3x²+5x | x⁵-2x⁴+6x³-2x²+ 5x

.                      -x⁵+ x⁴- 3x³-5x²

.                           - x⁴+3x³-7x²+ 5x

.                              x⁴-  x³+3x²+ 5x

.                                  2x³- 4x²+10x   → ÷ 2 = x³-2x²+5x  

.                 x+1                   .

x³-2x²+5x | x⁴ -  x³+3x²+5x

.                  -x⁴+2x³-5x²

.                          x³- 2x²+5x

.                        -x³-+2x²-5x

.                                 0

El m.c.d. de la fracción es  x³-2x²+5x.

Simplificando.  Dividiendo el numerador y el denominador entre el m.c.d. de la fracción:

.                   x³-1                                .

x³- 2x²+5x  | x⁶- 2x⁵+5x⁴-  x³+2x²-5x

.                  -x⁶+2x⁵-5x⁴

.                           0         -  x³+2x²- 5x   

.                                         x³- 2x²+5x

.                                                0

.                  x²+1                       .

x³- 2x²+5x | x⁵ - 2x⁴+6x³-2x²+5x

.                 - x⁵+ 2x⁴-5x³

.                                  x³-2x²+5x

.                                -x³+2x²- 5x

.                                        0

________________________________________

Ejercicio 121.

Simplificar hallando el m.c.d. de los dos términos:

.                             1                           .

a⁴-a³x-2a²x²+2ax³ | a⁴- a³x+ a²x²-  ax³

.                             -a⁴+a³x+2a²x²-2ax³

.                                           3a²x²-3ax³  → ÷ 3ax² = a - x

.                                     

.       a³-2ax²                  .

a -x | a⁴- a³x-2a²x²+2ax³

.       -a⁴+a³x

.                  -2a²x²+2ax³

.                    2a²x²-2ax³

.                           0

→ El m.c.d. de la fracción es a-x

 Simplificando la fracción, dividiendo sus miembros entre el m.c.d:

.        a³+ax²                  .

a -x | a⁴- a³x+a²x²-ax³

.      -a⁴+a³x

.           0     +a²x²-ax³ 

.                  -a²x²+ax³

.                         0 

.       a³-2ax²                 .

a -x | a⁴- a³x-2a²x²+2ax³

.       -a⁴+a³x

.            0    -2a²x²+2ax³

.                   2a²x²- 2ax³

.                          0

 

 

            

________________________________________

.                              1                         .

x⁴+3x³+6x²+3x+5 | x⁴+3x³+4x²-3x- 5

.                             -x⁴ -3x³ -6x²-3x- 5

.                                          -2x²-6x-10  → ÷ -2 = x²+3x+5

.               x²+1                      .

x²+3x+5 | x⁴+3x³+6x²+3x+5

.              -x⁴ -3x³ -5x²

.                              x²+3x+5

.                             -x² -3x-5

.                                    0

El m.c.d. de la fracción es x²+3x+5

Simplificando la fracción, dividiendo sus miembros entre el m.c.d.:

.               x²-1                     .

x²+3x+5 | x⁴+3x³+4x²-3x-5

.              -x⁴- 3x³ -5x²

.                            - x² -3x-5

.                              x²+3x+5

.                                    0

.               x²+1                     .

x²+3x+5 | x⁴+3x³+6x²+3x+5

.              -x⁴ -3x³ -5x²

.                               x²+3x+5

.                              -x² -3x-5 

.                                      0

______________________________________

 

6x³-13x²+18x-8 por 5    = 30x³-65x²+90x-40

10x³-9x²+11x+12 por 3 = 30x³-27x²+33x+36 

.                               1                            .

30x³-27x²+33x+36 | 30x³-65x²+90x-40

.                              -30x³+27x² -33x-36

.                                       -38x²+57x-76   → ÷ -19 = 2x²-3x+4

.                15x+9                     .

2x²-3x+4 | 30x³ -27x²+33x+36

.               -30x³+45x² -60x

.                          18x² -27x+36

.                         -18x²+27x -36

.                                    0

→ El m.c.d. de la fracción es 2x²-3x+4

Simplificando la fracción, dividiendo sus miembros entre el m.c.d.:

.                3x-2                   .

2x²-3x+4 | 6x³-13x²+18x -8

.               -6x³+ 9x² -12x

.                       -4x² + 6x  -8

.                        4x² -  6x +8

.                                0

.                5x+3                     .

2x²-3x+4 | 10x³ - 9x²+11x+12

.               -10x³+15x²-20x

.                            6x² - 9x+12

.                           -6x²+ 9x -12 

.                                     0

 

______________________________________

Multiplicando el numerador por 2 = 2x⁴-4x³y+4x²y²-2xy³

.                                1                               .

2x⁴-5x³y+4x²y²-xy³ | 2x⁴- 4x³y+4x²y²-2xy³

.                               -2x⁴+5x³y -4x²y²+ xy³

.                                          x³y             -xy³   → ÷ -xy = x²-y²

.         2x²-5xy+6y²           .

x²-y² | 2x⁴-5x³y+4x²y²  -xy³ 

.        -2x⁴         +2x²y²

.               -5x³y+6x²y² - xy³

.                5x³y           -5xy³ 

.                         6x²y² -6xy³

.                       -6x²y²          -6y⁴

.                                  -6xy³-6y⁴    → ÷ -6y³ = x -y 

.         x+y           .

x - y | x²        -y² 

.        -x²+xy 

.               xy -y²

.              -xy+y² 

.                    0

→  El m.c.d.de la fracción es x-y.

Simplificando la fracción:

.        x³-x²y+xy²             .

x -y | x⁴-2x³y+2x²y²-xy³

.       -x⁴-  x³y

.             -x³y+2x²y²

.              x³y -  x²y²

.                        x²y² -xy³

.                       -x²y²+xy³

.                              0

         2x³-3x²y+xy²          .

x -y | 2x⁴-5x³y+4x²y² -xy³

.      -2x⁴+2x³y

.             -3x³y+4x²y²

.              3x³y -3x²y² 

.                          x²y² -xy³

.                        - x²y²+xy³

.                               0

_______________________________________

M.C.D. de tres o más polinomios por divisiones sucesivas.

Para este caso hallamos el m.c.d. de dos polinomios como en el Ejercicio 113. y luego buscamos el m.c.d. del tercer polinomio y del m.c.d encontrado; y así sucesivamente, según la cantidad de polinomios del problema planteado. El m.c.d. solución será el último m.c.d encontrado.
____________________________________

Ejemplo.  

Hallar por divisiones sucesivas, el m.c.d de  2x³-11x²+10x+8 , 2x³+x²-8x-4  y  6ax²+11ax+4a.

m.c.d. de 2x³-11x²+10x+8 y 2x³+x²-8x-4

.                    1                          .

2x³+x²-8x-4 | 2x³-11x²+10x+  8

.                    -2x³-    x²+  8x+  4 

.                          -12x²+18x+12  → ÷ -6 = 2x²-3x -2

.                x+2                 .

2x²-3x -2 | 2x³+  x²- 8x- 4

.               -2x³+3x²+2x 

.                        4x²- 6x- 4

.                       -4x²+6x+4

.                               0 

→ el m.c.d. de 2x³-11x²+10x+8 y 2x³+x²-8x-4  es 2x²-3x -2

Buscando el m.c.d. de 2x²-3x -2  y 6ax²+11ax+4a. 

Antes le sacamos el factor común al tercer polinomio:

6ax²+11ax+4a.= a(6x²+11x+4) 

.                3                 .

2x²-3x -2 | 6x²+11x+ 4

.               -6x²+  9x+ 6

.                       20x+10   → ÷ 10 = 2x+1

.          x-2          :

2x+1 | 2x²-3x -2

.         -2x²-  x

.                -4x -2

.                 4x+2

.                     0

→ el m.c.d. de 2x³-11x²+10x+8 , 2x³+x²-8x-4  y  6ax²+11ax+4a  es 2x+1

_______________________________________

Ejercicio 114.

Hallar, por divisiones sucesivas, el m.c.d. de:

1) x³-2x²-5x+6 , 2x³-5x²-6x+9  y  2x²-5x-3

.                    2                         .

x³-2x²-5x+6 | 2x³- 5x² -  6x+ 9

.                    -2x³+4x²+10x-12

.                            - x² + 4x-  3  → ÷ -1 = x² -4x +3

.                x+2                  .

x² -4x +3 | x³- 2x²-5x+6

.               -x³+4x²-3x

.                      2x²-8x+6

.                    -2x²+8x- 6

.                             0

→ el m.c.d de los 2 primeros polinomios es x² -4x +3

.                2             .

x² -4x +3 | 2x²- 5x-3

.               -2x²+8x-6

.                        3x-9    → ÷ 3 = x-3

.      x-1           .

x-3 | x²-4x +3

.     -x²+3x

.            - x+3

.              x- 3

.                 0

→  el m.c.d de los tres polinomios es x-3.

_____________________________________

2) 2x³-x²y-2xy²+y³  ,  8x³+6x²y-3xy²-y³  y  6x²-xy-y²

.                           4                              .

2x³-x²y-2xy²+y³ | 8x³+ 6x²y- 3xy²-  y³

.                          -8x³+ 4x²y+8xy²-4y³

.                                  10x²y+5xy²-5y³  → ÷ 5y = 2x²+xy-y²

.                 x                         .

2x²+xy-y² | 2x³- x²y-2xy²+y³

.                 -2x³- x²y-  xy²

.                       -2x²y-  xy²+y³  → ÷ -y = 2x² +xy -y² 

                     1               .

2x² +xy -y²  | 2x²+xy-y²

.                   -2x²- xy+y²

.                           0

→ El m.c.d. de los primeros dos polinomios es 2x² +xy -y²

.                   3               .

2x² +xy -y² | 6x²- xy-   y²

.                  -6x²-3xy+3y²

.                        -4xy+2y²  → ÷ -2y = 2x-y

.         x+y            .

2x-y | 2x²+xy-y²

.        -2x²+xy

.               2xy- y²

.              -2xy+y²

.                    0

→ El m.c.d. de los tres polinomios es 2x-y.

_____________________________________

3) x⁴+x³-x²-x  ,  2x³+2x²-2x-2  y  5x³-5x²+2x-2

Sacando el factor común de x⁴+x³-x²-x = x(x³+x²-x-1)

.                 2                    .

x³+x²-x-1 | 2x³+2x²- 2x- 2

.                -2x³- 2x²+2x+2

.                           0

→ El m.c.d. de los primeros dos polinomios es x³+x²-x-1

.                5                     .

x³+x²-x-1 | 5x³- 5x²+2x -2

.                -5x³- 5x²+5x+5

.                      -10x²+7x+3  → ÷ -1 = 10x²-7x-3

y,  (x³+x²-x-1) (10) = 10x³+10x²-10x-10 

.                 x                            .

10x²-7x-3 | 10x³+10x²-10x-10

.                -10x³+  7x²+ 3x

.                           17x²-  7x-10

→ (17x²-7x-10)(10) = 170x²-70x-100

y,  (10x²-7x-3)(17)   = 170x²-119x-51

.                         1                      .

170x²-70x-100 | 170x²-119x-  51

.                        -170x²+ 70x+100

.                                   -  49x+ 49  → ÷ -49 = x-1 

.        170x+100            

x -1 | 170x² -  70x- 100

.       -170x²+170x

.                    100x- 100

.                   -100x+100

.                            0

→ El m.c.d. de los tres polinomios es x -1

_______________________________________

4) 3a⁴-9a³x+4a²x²-3ax³+2x⁴ , a⁴+3a³x+a²x²-3ax³-2x⁴  y  4a³+8a²x-ax²-2x³

.                                     3                                      .

a⁴+3a³x+a²x²-3ax³-2x⁴ | 3a⁴-9a³x+4a²x²- 3ax³+2x⁴

.                                    -3a⁴-9a³x- 3a²x²+9ax³+6x⁴

.                                                       a²x²+6ax³+8x⁴  → ÷ x²=a²+6ax+8x²

.                    a²-3ax+11x²                        .

a²+6ax+8x² | a⁴+3a³x+   a²x² -  3ax³-  2x⁴

.                   -a⁴- 6a³x-  8a²x²

.                        -3a³x - 7a²x² -  3ax³

.                         3a³x+18a²x²+24ax³

.                                   11a²x²+21ax³-  2x⁴

.                                  -11a²x²- 66ax³-88x⁴

.                                              -45ax³-90x⁴  =  -45x³(a+2x)

.           a+4x           .

a +2x | a²+6ax+8x²

.          -a²- 2ax 

.                4ax+8x² 

.               -4ax- 8x²

.                       0                              

→ El m.c.d. de los dos primeros polinomios es a+2x.

.          4a²-x²                   .

a+2x | 4a³+8a²x-ax²-2x³

.         -4a³- 8a²x

.                         -ax²-2x³

.                          ax²+2x³

.                                0

→ El m.c.d. de los tres polinomios es a+2x.

______________________________________

M.C.D. de dos polinomios por divisiones sucesivas.

Este es el método que se utiliza para hallar el m.c.d. de dos polinomios, que no pueden factorizarse fácilmente.

Regla para encontrar el m.c.d. de dos polinomios por divisiones sucesivas:

Se ordenan ambos polinomios con relación a una misma letra y se divide el de mayor grado entre el de grado menor. 

 

Cuando ambos son del mismo grado, cualquiera se toma como dividendo. 

Si la división no es exacta se divide el divisor entre el primer residuo, y así sucesivamente hasta llegar a un residuo cero.  El ultimo divisor será el m.c.d. buscado.

Cada división termina hasta que el grado del primer término del residuo sea menor que el grado del primer término del divisor. 

______________________________________

Ejemplo a)
Hallar por divisiones sucesivas el m.c.d. de 16x³+36x²-12x-18 y 8x²-2x-3

Dividiendo el polinomio de mayor grado entre el de menor:

.                2x+5                         .

8x²-2x-3  | 16x³+36x² -12x -18

.                -16x³+  4x² + 6x

.                           40x² -  6x -18

.                          -40x²+10x+15

.                                       4x -  3  Residuo

Dividiendo el divisor entre el residuo, de la primera división.

.          2x+1          .

4x -3  | 8x²- 2x -3 

.          -8x²+6x   

.                   4x -3

.                  -4x+3

.                       0

La división es exacta por lo tanto el m.c.d. es 4x -3

____________________________________

Ejemplo b).

Hallar, por sucesiones sucesivas, el m.c.d. de

12x³-26x²+20x-12  y  2x³-x²-3x

Dividiendo el primer polinomio entre 6 y el segundo entre x:

= 6x³-13x²+10x-6 ÷  2x²-x-3

.             3x-5                              .

2x²-x-3 | 6x³-13x²+10x - 6

.             -6x³+ 3x²+  9x

.                    -10x²+19x- 6

.                     10x² -  5x-15

.                               14x-21

Dividiendo el residuo 14x-21 entre 7 = 2x-3                        

--> 2x²-x-3 ÷  2x-3

..        x+1           .

2x-3 | 2x² -  x-3

.        -2x²+3x

.                 2x -3

.                -2x+3

.                     0

La división es exacta por lo tanto el m.c.d. es 2x-3

_____________________________________

Ejemplo c)

Hallar, por divisiones sucesivas, el m.c.d. de 3x³-13x²+5x-4  y  2x²-7x-4

El 3x³ no es divisible entre 2x², entonces se multiplica el primer polinomio por 2 para que sea divisible:

=> la división sería:

6x³-26x²+10x-8 ÷  2x²-7x-4

.               3x                       .

2x²-7x-4 | 6x³-26x²+10x -8

.              -6x³+21x²+12x

.                      - 5x²+22x -8

Como -5x² no es divisible entre 2x², entonces le cambiamos el signo, y sería 5x²-22x +8 y lo multiplicamos por 2 para que sea divisible entre 2x², quedaría 10x²-44x +16

--> 10x²-44x +16 ÷  2x²-7x-4

.               5                      .

2x²-7x-4 | 10x²-44x +16

.              -10x²+35x+20

.                         - 9x+36

.Se cambia el signo al residuo y sería 9x-36 y lo dividimos entre 9 y quedaría x-4

--> 2x²-7x-4 ÷  x-4

.       2x+1              .

x -4 | 2x² -7x -4

.       -2x²+8x

.                  x -4

.                 -x+4

.                    0

La división es exacta, por lo tanto el m.c.d. es x -4. 

_______________________________________

Ejercicio 113.

Hallar por divisiones sucesivas el m.c.d. de:

1) 12x²+8x+1  y  2x²-5x-3

.                6                  .

 2x²-5x-3 | 12x²+  8x+ 1

.               -12x²+30x+18

.                          38x+19  --> (38x+19) ÷19 = 2x+1

.         x-3         .

2x+1 | 2x²-5x-3

.         -2x² - x

.                -6x -3

.                 6x +3

.                     0

--> m.c.d. es  2x+1

______________________________

2) 6a²-2a-20  y  2a³-a²-6a

Se divide 2a³-a²+6a entre "a" y es 2a²-a-6

.             3             .

2a²-a-6 | 6a² -2a -20

.            -6a²+3a+18

.                        a- 2

.       2a+3      .

a -2 | 2a² - a -6

.      -2a²+4a

.               3a -6

.              -3a+6

.                  0

--> el m.c.d. es a-2.

______________________________

3) 5a³-6a²x+ax²  y  3a³-4a²+ax²

Sacando el factor común de ambos polinomios:

5a³-6a²x+ax² = a(5a²-6ax+x²)

3a³-4a²+ax²   = a(3a²-4ax+x²)

--> El primer factor común del m.c.d. de ambos polinomios es "a".

Por consiguiente los polinomios a determinar el m.c.d. son:

5a²-6ax+x²  y  3a²-4ax+x²

Antes multiplicamos 5a²-6ax+x² por 3, para poder dividirlos entre 3a²-4ax+x²:y es = 15a²-18ax+3x²:

.                  5                      .

3a²-4ax+x² | 15a²-18ax+3x²

.                  -15a²+20ax-5x²

.                               2ax-2x²   (Dividimos entre 2x para simplificarlo = (a-x)

.        3a -x         .

a -x | 3a² -4ax+x²

.       -3a²+3ax

.               - ax+x²

.                 ax -x²

.                     0

--> El segundo factor común de ambos polinomios es a -x

Por lo tanto el m.c.d. de los polinomios es a(a-x).

____________________________________

4) 2x³+4x²-4x+6  y  x³+x²-x+2

.                 2                     .

x³+x²-x+2 | 2x³+4x²-4x+6

.                 -2x³-2x²+2x -4

.                         2x² -2x+2  (Dividimos entre 2 para simplificarlo = x²-x+1

.            x +2         .

x²-x+1 | x³+x² - x+2

.           -x³+x² - x

.                2x²-2x+2

.               -2x²+2x-2

.                      0

--> El m.c.d. de los polinomios es x²-x+1.

____________________________________

5) 8a⁴-6a³x+7a²x²-3ax³  y  2a³+3a²x-2ax²

Sacando el factor común de ambos polinomios:

8a⁴-6a³x+7a²x²-3ax³ = a(8a³-6a²x+7ax²-3x³)

2a³+3a²x-2ax² =  a(2a²+3ax-2x²)

--> El primer factor común del m.c.d. de los polinomios es "a".

.                    4a-9x                      .

2a²+3ax-2x² | 8a³-  6a²x+  7ax²- 3x³ 

.                    -8a³-12a²x+  8ax²

.                          -18a²x+15ax²- 3x³

.                           18a²x+27ax²-18x³

.                                      42ax²-21x³  (Dividiendo entre 21x² para simplificarlo=2a-x

.         a+2x             .

2a -x | 2a²+3ax -2x²

.         -2a²+  ax

.                 4ax -2x²

.                -4ax+2x²

.                        0

El 2º factor común de los polinomios es 2a-x.

Por lo tanto, el m.c.d. de los polinomios es = a(2a-x)

_____________________________________

9) 2m⁴-4m³-m²+6m-3  y  3m⁵-6m⁴+8m³-10m²+5m

(3m5-6m⁴+8m³-10m²+5m)(2) = 6m⁵-12m⁴+16m³-20m²+10m

--> 

.                                3m                                        .

2m⁴-4m³-m²+6m-3 | 6m⁵ -12m⁴+16m³-20m²+10m

.                               -6m⁵+12m⁴+  3m³-18m²+  9m

.                                                    19m³-38m²+19m  ÷19 = m³-2m²+m

.                  2m                          .

m³-2m²+m | 2m⁴ -4m³-  m²+6m-3

.                  -2m⁴+4m³-2m²

.                                  -3m²+6m-3  ÷ -3 = m²-2m+1

.                m               .

m²-2m+1 | m³-2m²+m

.                -m³+2m²-m

.                        0

El m.c.d. de los polinomios es m²-2m+1

____________________________________