Es convertir una fracción en otra equivalente de numerador o denominador dado; donde el nuevo numerador o denominador sea múltiplo del numerador o denominador de la fracción original.
Si nos dan un numerador equivalente al original; debemos multiplicarlo por el cociente del numerador dado entre el numerador original, pero también debemos multiplicar ese cociente por el denominador dado.
También puede ser a la inversa si lo que se pide es cambiar el denominador de la fracción original.
Si la fracción es equivalente a otra dada, es porque no varía si sus dos términos son multiplicados por una misma cantidad.
Ejemplos: 3/6 ≡ 1/2, porque 3/6 = 0.5 y 1/2 = 0.5
_______________________________________
Ejemplos:
a) Reducir 2a/3b a fracción equivalente de numerador 6a²
Encontrado el cociente de los numeradores y multiplicando la fracción por este.
6a² ÷ 2a = 3a ⇒
(2a)(3a) / (3b)(3a)
= 6a²/ 9ab Fracción equivalente.
_______________________________________
b) Convertir 5 / 4y³ en fracción equivalente de denominador 20a²y⁴.
Encontrado el cociente de los denominadores y multiplicando la fracción por este.
20a²y⁴ ÷ 4y³ = 5a²y ⇒
5( 5a²y) / 4y³(5a²y)
= 25y³ / 20a²y⁴ Fracción equivalente.
Nota:_ Al simplificar 25y³ / 20a²y⁴ nos daría 5y³ / 4a²y⁴ , que es otra fracción equivalente.
_______________________________________
c) Reducir x-2 / x-3 a fracción equivalente de denominador x² -x -6
Encontrado el cociente de los denominadores y multiplicando la fracción por este.
x² -x -6 / x-3
= (x-3)(x+2) / x-3
= x+2 Cociente ⇒
(x-2)(x+2) / (x-3)(x+2)
= x² -4 / x² -x -6 Fracción equivalente.
______________________________________
Ejercicio 122.
Completar:
1)
4a² ÷ 2a = 2a ⇒
 Fracción equivalente.
Fracción equivalente.
 Fracción equivalente.
Fracción equivalente.
 Fracción equivalente.
Fracción equivalente. 

 Fracción equivalente.
Fracción equivalente.
15 ÷ 5 = 3 ⇒


 Fracción equivalente.
Fracción equivalente.

(a+b)(a+b) ÷ a+b = a+b
 Fracción equivalente.
Fracción equivalente.
 Fracción equivalente.
Fracción equivalente. 
2a³ ÷ 2a = a² ⇒
 Fracción equivalente.
Fracción equivalente.
12 ÷ 6 = 2 ⇒
 Fracción equivalente.
Fracción equivalente.
 Fracción equivalente.
Fracción equivalente.

 Fracción equivalente.
Fracción equivalente.
 Fracción equivalente.
Fracción equivalente.

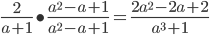 Fracción equivalente.
Fracción equivalente.
 Fracción equivalente.
Fracción equivalente.
 Fracción equivalente.
Fracción equivalente.
 Fracción equivalente.
Fracción equivalente.
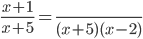



No hay comentarios.:
Publicar un comentario
Sugiere, solicita o comenta. Es muy importante.