Procedimiento:
Ejemplos:
Simplificar:
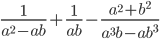
a²-ab = a(a-b)
ab = ab
a³b-ab³ = ab(a²-b²) = ab(a-b)(a+b)
-> el m.c.m. es ab(a-b)(a+b)
Dividiendo el m.c.m. entre cada uno de los denominadores:
ab(a-b)(a+b) ÷ a(a-b) = b(a+b)
ab(a-b)(a+b) ÷ ab = (a-b)(a+b)
ab(a-b)(a+b) ÷ ab(a²-b²) = 1
Multiplicando cada uno de los cocientes entre su respectivo numerador, escribiéndolos uno después del otro separados por el signo de cada fracción y como un solo denominador de todo se pone el m.c.m, y simplificando:
______________________________________
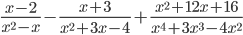
Hallando el m.c.m :
x²-x = x(x-1)
x²+3x-4 = (x+4)(x-1)
x⁴+3x³-4x² = x²(x²+3x-4) = x²(x+4)(x-1)
-> El m.c.m. es x²(x+4)(x-1)
∴ x²(x+4)(x-1) ÷ x(x-1) = x(x+4)
x²(x+4)(x-1) ÷ (x+4)(x-1) = x²
x²(x+4)(x-1) ÷ x²(x+4)(x-1) = 1
Multiplicando cada uno de los cocientes entre su respectivo numerador, escribiéndolos uno después del otro separados por el signo de cada fracción y como un solo denominador de todo se pone el m.c.m, y simplificando.
______________________________________
x+2 = x+2
x²-x-6 = (x-3)(x+2)
m.c.m. es (x-3)(x+2)
(x-3)(x+2) ÷ x-3 = x+2
(x-3)(x+2) ÷ x+2 = x-3
(x-3)(x+2) ÷ (x-3)(x+2) = 1
_____________________________________
3a+6 = 3(a+2)
6a+12 = 6(a+2)
12a+24 = 12(a+2)
m.c.m. es 12(a+2)
12(a+2) ÷ 3(a+2) = 4
12(a+2) ÷ 6(a+2) = 2
12(a+2) ÷ 12(a+2) = 1
_____________________________________
x²+1 = x²+1
3x = 3x
x² = x²
m.c.m. es 3x²(x²+1)
3x²(x²+1) ÷ x²+1 = 3x²
3x²(x²+1) ÷ 3x = x(x²+1)
3x²(x²+1) ÷ x² = 3(x²+1)
______________________________________
a²-1 = (a-1)(a+1)
2a+2 = 2(a+1)
4a-4 = 4(a-1)
m.c.m. es 4(a-1)(a+1)
4(a-1)(a+1) ÷ (a-1)(a+1) = 4
4(a-1)(4+1) ÷ 2(a+1) = 2(a-1)
4(a-1)(a+1) ÷ 4(a-1) = (a+1)
_____________________________________
a²+ab = a(a+b)
ab = ab
ab+b² = b(a+b)
m.c.m. es ab(a+b)
ab(a+b) ÷ a(a+b) = b
ab(a+b) ÷ ab = (a+b)
ab(a+b) ÷ b(a+b) = a
____________________________________
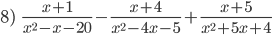
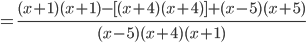
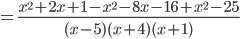
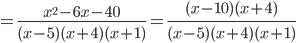
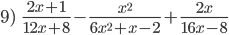
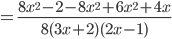
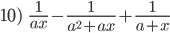


























No hay comentarios.:
Publicar un comentario
Sugiere, solicita o comenta. Es muy importante.